[물리실험] 미급감쇠조화운동

1. 실험목적
미급감쇠하는 진동자의 운동의 특성을 살펴보고, 한 주기 당 감쇠되는 에너지의 양을 측정하여 Q-인수(Quality factor)를 구한다.
2. 실험원리
1) 감쇠조화운동
평형점부터의 변위를 x라 하면 복원력은 -kx이고 제동력은 -cẋ이다. c는 비례상수이다. 그러므로 운동에 관한 미분방정식은 mẍ+cẋ+kx=0 이다.
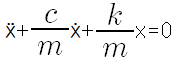
감쇠인자 γ를 다음과 같이 정의하여

이 인자와

을 식에 대입하면 방정식은 다음과 같게 된다.

미분연산자d/dt를 D로 표기하면

연산자를 인수분해하면,
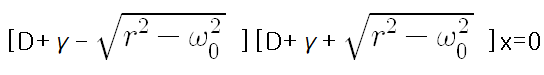
따라서
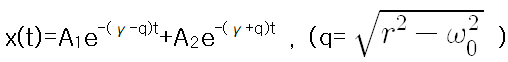
이다.
여기서
i. q>0 이면, 과다감쇠
ii. q가 허수이면, 미급감쇠
가 된다.
(q=0일 때는 임계감쇠로서, 해가
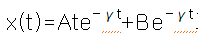
가 된다. 실험내용과 큰 관련이 없으므로 계산과정은 생략한다.)
q가 허수일 때, 풀이를 실수로 만들면,
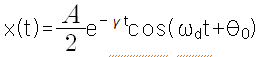
가 된다.
2) Q인수
약하게 감쇠 진동하는 조화진동자의 에너지 손실률은 진동자의 Q인수로 기술된다. Q인수는 한 진동주기 Td동안 진동자의 전체 에너지를 손실된 에너지로 나눈 후 2π를 곱한 값으로 정의한다. 진동자가 약하게 감쇠 한다면 한 주기 동안 에너지 손실은 작고 다라서 Q인수는 커진다.
3) 미급감쇠그림(1m가 넘는 임의길이의 진자)
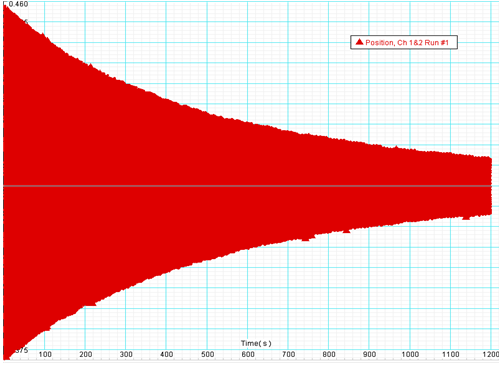
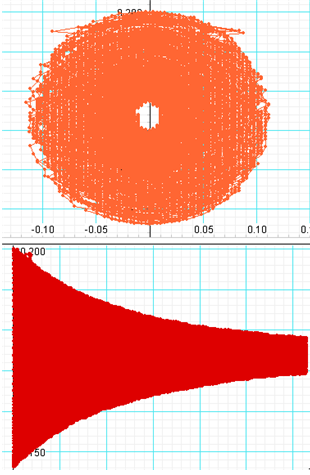
x-t그래프의 가로축을 축소하여 덮개선만 본 그림이다.
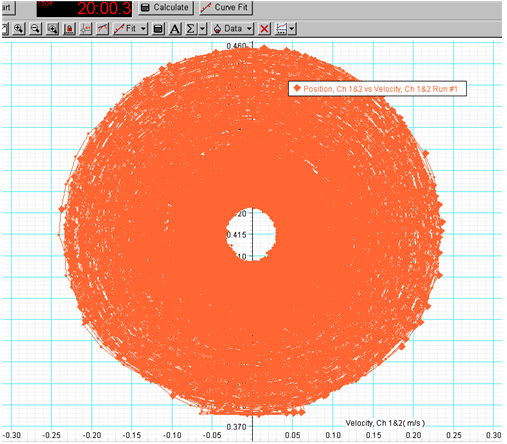
v-x 위상공간 그래프이다. 안쪽으로 갈수록 점의 밀 도가 높아지는 것이 보인다.
* 위상공간에서의 감쇠조화진동자
a.감쇠력이 없는 경우
단조화 진동자에서 시간의 함수로 위치와 속도는 다음과 같다.
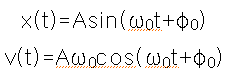
윗 식에서 t를 소거하면 위상 공간에서 진동자의 궤적을 알 수 있다.
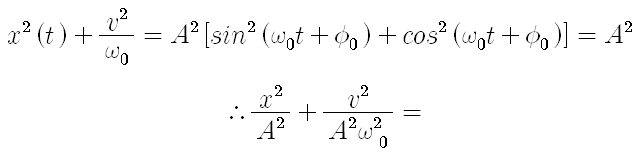
이것은 장반경과 단방경이

인 타원의 방정식이다.
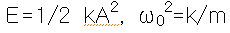
을 대입하면

을 얻는데

이것이 바로 에너지 방정식이 된다.
그러므로 닫힌 궤적은 각각 특정한 전체의 역학 에너지에 해당한다.
b.미급감쇠조화진동자
미급감쇠조화진동자의 위상공간에서의 궤적은 다음과 같다.
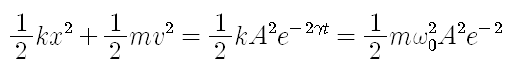
한편, 어느 순간 진동자에 저장된 에너지는 다음과 같다.

이 식과 비교하면 임의의 순간 진동자에 잔류하는 에너지는 다음과 같다.

약하게 감쇠하는 조화 진동자의 에너지는 시간 상수

를 가지고 지수적으로 약해져서 소멸한다. 위상 공간의 안쪽으로 오므라드는 것은 이 사실을 반영한다.
c. 각각 1분, 3분, 5분, 7분, 9분에서의 미급감쇠진동자의 v-x위상공간에서의 궤적. 시간이 갈수록 그래프의 안쪽을 그리는 것을 알 수 있다.(60cm진자. 9분은 짧아서 실험데이터로 쓰이지는 않았음)

3. 실험과정
1) 인터페이스 실험 장치를 이용하여 대략 20분간 진자를 진동시킨다.
2) 진폭의 최대값이 처음의 절반이 되는 시간을 찾는다. 또한, 1/4이 되는 시간도 찾는다. 두 값의 기하평균값을 구하여 진폭의 반감기를 측정한다.
3) 진자의 주기를 구하여, 반감기 구간동안에 진자가 몇 주기 진동했는지 구한다. 진폭의 반감기는 에너지가 1/4이 되는 시간이므로, 진동한 회수 제곱근(300번 진동이면

을 구하면, 한 주기당 손실된 에너지 비인 ∆E/E를 구할 수 있다.
4) 정의를 이용하여 c에서 구한 값의 역수에 2π를 곱하여 구할 수 있다.

4. 실험결과
(두 번째 그래프의 시간축을 보며 비교해 보세요.)
(1) 30cm진자
첫 번째 실험
진동축=0.239m(그래프의 linear fit으로 구한다.)
처음진폭=0.255-0.239(m)
첫 번째 반감기=90.0283초(0.247-0.239(m))
두 번째 반감기=84.8346초(0.243-0.239(m))
세 번째 반감기=121.7100초(0.241-0.239(m))
평균(기하평균)=97.59초
주기=1.102초
진동한 수=88.56주기

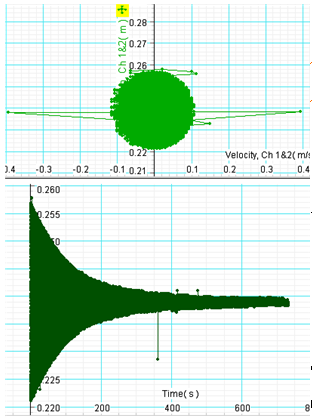
두 번째 실험
진동축=0.241
처음진폭=0.257-0.241(m)
첫 번째 반감기=95.2925초(0.249-0.241(m))
두 번째 반감기=122.6934초(0.245-0.241(m))
평균(기하평균)=108.13초
주기=1.108초
진동한 수=97.59주기
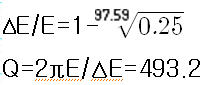

(2) 60cm진자
첫 번째 실험
진동축=0.173
처음진폭=0.173-0.146(m)
첫 번째 반감기=174.9533초(0.173-0.1595(m))
두 번째 반감기=225.9078초(0.173-0.1663(m))
세 번째 반감기=224.9551초(0.173-0.1697(m))
평균(기하평균)=207.17초
주기=1.565초
진동한 수=132.38주기

두 번째 실험
진동축=0.193
처음진폭=0.193-0.156(m)
첫 번째 반감기=200.5421초(0.193-0.1745(m))
두 번째 반감기=220.9323초(0.193-0.1838(m))
세 번째 반감기=289.5793초(0.193-0.1883(m))
평균(기하평균)=234.105초
주기=1.5040초
진동한 수=155.66주기


(3) 90cm진자
첫 번째 실험
진동축=0.264
처음진폭=0.364-0.264(m)
첫 번째 반감기=324.5728초(0.314-0.264(m))
두 번째 반감기=294.0909초(0.289-0.264(m))
세 번째 반감기=368.3219초(0.277-0.264(m))
평균(기하평균)=327.58초
주기=1.9120초
진동한 수=171.33주기


두 번째 실험
진동축=0.260
처음진폭=0.260-0.149(m)
첫 번째 반감기=341.0840초(0.260-0.214(m))
두 번째 반감기=342.1014초(0.260-0.289(m))
세 번째 반감기=399.1774초(0.260-0.277(m))
평균(기하평균)=359.80초
주기=1.9143초
진동한 수=187.95주기


실험오차를 줄이는 법(그래프가 잘 나오게 하는 법)
1. 기본적으로 진동면이 하나로 정해지면서 잡 떨림이 없도록 잘 흔들어야 한다. 이는 처음에 손으로 잡다가 떼는 법 보다는 진자를 어떤 물체로 떠받치다가 원하는 진동면으로 빠르게 떼는 방법이 더 적당하다. 그리고 진자의 실의 꼬임에 의해 회전하게 되면 안 된다.
2. 진자의 운동은 실제 직선이 아니라 직선에 가까운 원의 일부 구간이다. 따라서 진폭이 크면 가장 높은 곳과 낮은 곳의 차이에 의해 센서가 측정을 잘하지 못하게 된다.
3. 우선, 적당한 진폭으로 흔들기 전에 추의 높이는 센서의 음파가 발사되는 원의 중앙에 위치할 정도의 높이가 가장 적당하다. 실제, 실험을 해보면, 가장 낮은 지점의 측정이 잘 되지 않는데, 처음 진폭이 없을 때의 추의 위치가 바로 가장 낮은 지점인 동시에 속도가 가장 빠른 구간이기 때문이다. 정중앙에 있을 때가 가장 측정을 잘 할 것이다.
4. 우선 진자를 먼저 진동을 시킨 뒤, 예비로 측정을 하여 나온 그래프를 이용하여 진자와 모션 센서의 위치를 조정하자. 주기측정 같이 비교적 간단한 실험의 경우는 위치그래프만 제대로 나와도 정확한 실험이 가능하다. 하지만, 감쇠진동 실험을 할 때, 위치-속도 위상공간에서 깔끔한 데이터를 얻으려면 속도 그래프의 오차도 고려해야 한다. 예시로 방법을 설명하면 다음과 같다.
5. 이 그래프(v-t그래프)에서는 그래프의 끝 부분, 즉 속력이 가장 빠른 구간에서 측정이 잘 되지 않음을 알 수 있다. 일반적인 경우로서, 사실 가장 해결이 어려운 문제이기도 하다. 모션센서의 각도를 아주 약간 낮추거나, 스탠드를 약간 올려 진자를 높은 곳에서 진동하게 하여야 한다.
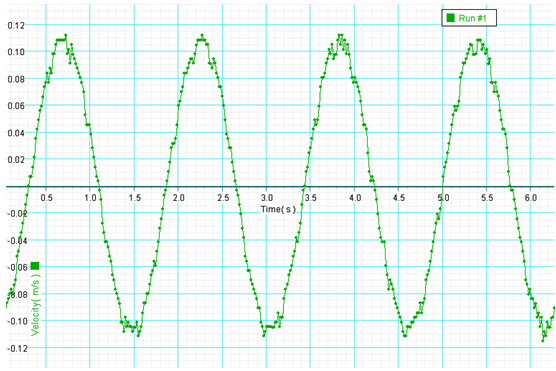

이 그래프(v-t그래프)에서는 사인형 그래프의 오른쪽, 즉 가속도가 음이면서 진동축에서 모션센서와 반대쪽 부분이 측정이 잘 되지 않음을 알 수 있다. 센서를 약간 진자에 가까이 하거나, 추를 약간 낮추거나, 모션센서의 각도를 아주 약간 높여야 한다. 진동면과 모션센서가 일치하지 않아도 일어난다.
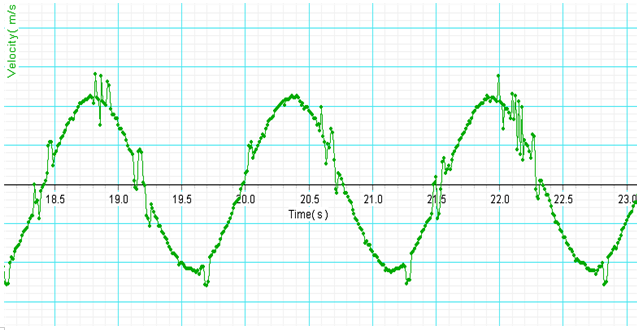
이 v-t그래프에서는 시간축 근처, 즉 속도가 느린 끝 부분에서 측정이 잘 되지 않음을 알 수 있다. 약간 추가 높은 경우에 있을 수 있다.
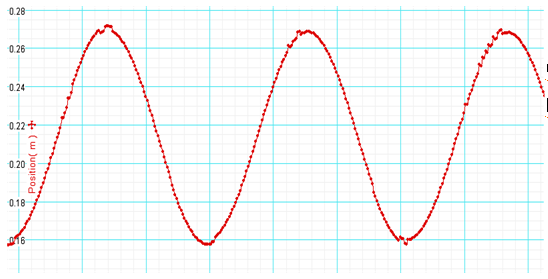
앞의 속도시간 그래프와 같은 시간의 x-t그래프 이다. 역시 끝부분에 약간의 요철을 발견할 수 있다.
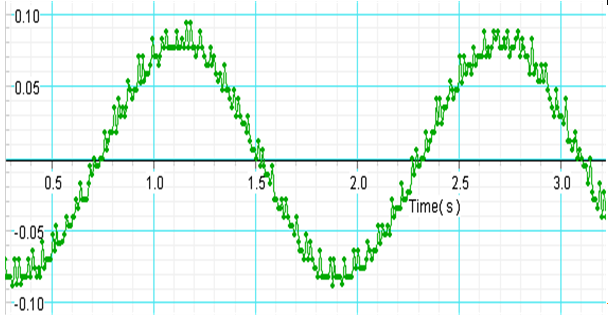
이 그래프는 전체적으로 실험이 잘 된 듯하지만, 그래프에 전체적인 요동이 있음을 알 수 있다. 이 경우는 원인을 잘 알기 힘들었다. 이 요동은 어떠한 경우로도 사라지게 하기는 힘들었다. 추의 미세한 요철에 의해 생기는 것이 아닌가 추측이 가기도 한다. 아니면 센서의 위치 측정 정밀도에 의해 이렇게 될 수 있을 것 같기도 하다.(이 그래프를 자세히 보면 어떤 속도 값 사 이에는 어떠한 값도 없이 계단모양으로 되어있 는데, 위치도 그래프를 벌리면 그 정도가 매우 작지만, 수치가 계단 형으로 되어있다.)

이 그래프처럼 약간 진폭을 크게 해주면 문제가 어느 정도 해결된다.(사실 요동이 없어지지는 않으며 그래프의 크기에 묻히는 것이다.) v-t 그래프가 이정도 수준으로 나오면 x-t그래프는 아주 깔~끔하게 나오게 된다. (아래 그래프)

2021.09.14 - [물리실험] MBL을 이용한 공기 저항계수 및 종단속도 측정
[물리실험] MBL을 이용한 공기 저항계수 및 종단속도 측정
[물리실험] MBL을 이용한 공기 저항계수 및 종단속도 측정 Ⅰ. 실험목표 가속도 센서를 이용하여 저항이 있는 공기 내에서 물체가 수직으로 떨어질 때 물체가 받는 공기 저항의 계수를 구할 수 있
orange025.tistory.com
2021.09.14 - [물리 실험] MBL을 활용한 충격량과 운동량 보존 법칙 실험
[물리 실험] MBL을 활용한 충격량과 운동량 보존 법칙 실험
[물리 실험] MBL을 활용한 충격량과 운동량 보존 법칙 실험 Ⅰ. 실험목표 인터페이스를 이용한 1차원 충돌실험으로 충격량과 운동량의 관계를 이해하고 설명할 수 있고 2차원 충돌 실험에서 운동
orange025.tistory.com

'여기는 과학실 > 과학실험 이야기' 카테고리의 다른 글
| [물리실험] MBL을 활용한 정지마찰계수 측정 (0) | 2021.09.18 |
|---|---|
| [물리실험] 반발계수의 측정 (0) | 2021.09.17 |
| [물리실험] 단진동 운동 (0) | 2021.09.15 |
| [물리실험] MBL을 이용한 공기 저항계수 및 종단속도 측정 (1) | 2021.09.14 |
| [물리 실험] MBL을 활용한 충격량과 운동량 보존 법칙 실험 (0) | 2021.09.14 |



